「唯一需要恐懼的是恐懼本身」是個愚蠢的建議。

當然不用去囤購衛生紙，但如果政策制定者害怕恐懼的話，他們就會降低真實的危險來避免「集體恐慌」。恐懼本身不是問題，問題是我們如何轉化我們的恐懼，恐懼給我們對付當下危險的力量，並且為未來的危機做準備。

老實說我們（流行病學家 Marcel＋Nicky 美術／程式）很擔心，我們猜你也是！這是為什麼我們將恐懼化為製作這些可互動模擬的動力，讓你們可以將恐懼化為瞭解。

• 接下來的幾週（流行病學 101、SEIR 模型、R和R₀）
• 接下來的幾個月（封鎖、接觸追蹤、口罩）
• 接下來的數年（失去免疫力？沒有疫苗？）

這份指南（2020年5月1日出版，點擊註腳！→¹）的主旨是要給你盼望和恐懼。為了以 確保我們心理健康及財政健全 的方式打敗新冠病毒，我們需要樂觀地制定計劃，並且悲觀地制定備案。正如 Gladys Brownwyn Stern 曾說過的：「樂觀者發明飛機，悲觀者發明降落傘。」

所以請繫好安全帶，我們將遭遇亂流。

之前的幾個月

飛行員用飛行模擬器來避免如何避免飛機失事。

流行病學家使用傳染病模擬器來避免人類滅亡。

所以讓我們來做一個非常、 非常 簡單的「傳染病飛行模擬器」！在這個模擬中傳染者 可以將疾病傳播給易感者 ，因而產生更多傳染者 ：

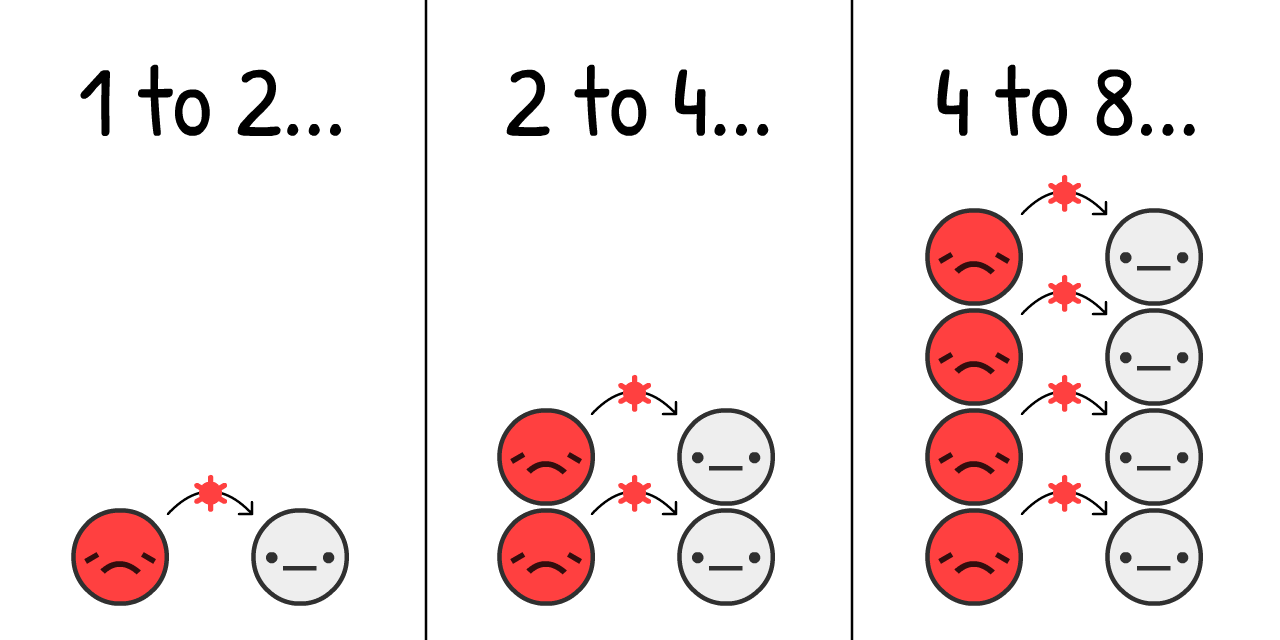
經過估計，在 COVID-19 爆發初期， 平均 每四天病毒從一個 傳播到一個 ² (記住這有很多變因)

如果我們 只用 「每四天傳染者增加一倍」這個條件在只有 0.001% 傳染者 的初始條件下，會發生什麼事？

點擊「開始」來遊玩！你可以在之後以不同的條件再玩一次： （警告：³）

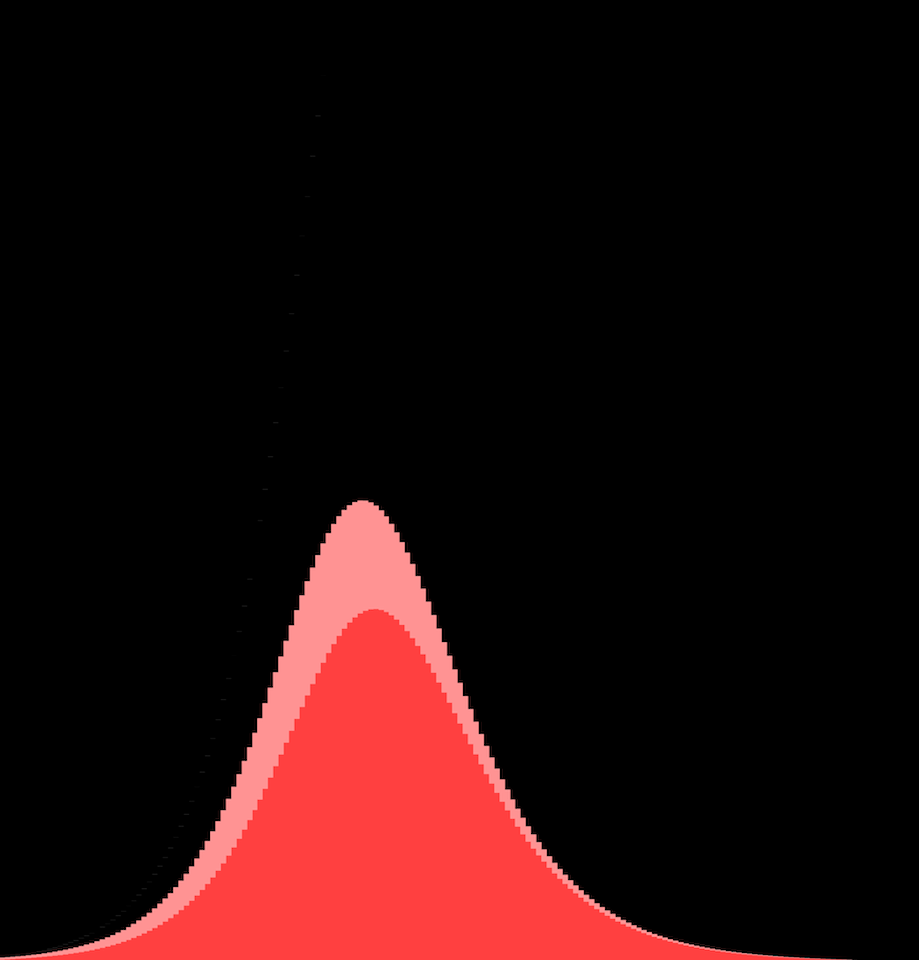
這是一條 指數增長的曲線 。一開始很小、然後爆炸。從「喔這只是流感」到「喔對啦，流感不會讓富裕的城市出現萬人塚。」

但這個模擬是錯的。幸好指數增長不能永遠持續。其中一件阻止病毒傳播的因素是其他人是否 已經 得到這個病毒。

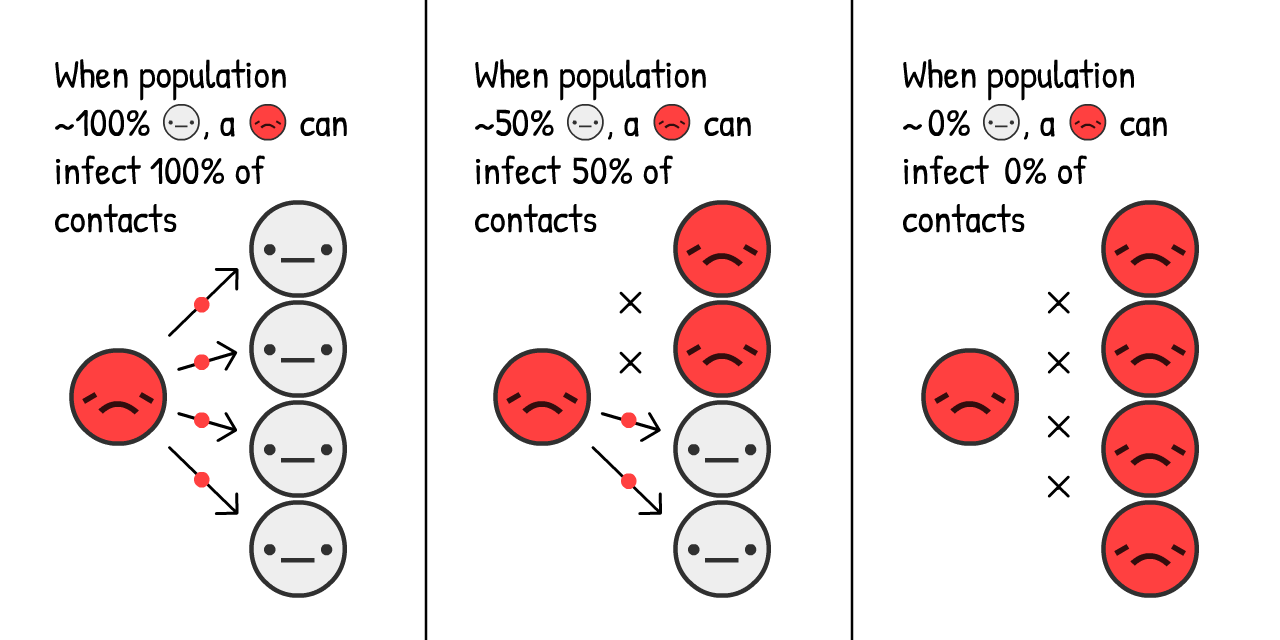
越多 的時候, 越快變成 ， 但 越少的時候， 越慢 變成 。

這如何改變疫情的增長呢？讓我們試試看：

這是一條「S型」的 邏輯增長曲線（logistic growth curve） ，一開始很小、爆炸性增長、然後增長重新慢下來。

但這個模擬 依然 不對，我們忽略患者最後將不再具有傳染性，不管是因為患者 1) 復原 2) 帶著肺損傷的「復原」 3) 死亡。

為了簡化問題，我們假設所有的 都將復原 （只要記得在現實中有些人過世了）。 不再會被傳染，並且讓我們假設—只有現在假設！—他們終身免疫。

根據估計，如果你得到 COVID-19，平均來說你有10天處在傳染期 。⁴這意味著有些人在10天內復原，有些人需要更長的時間。 這是初始條件為 100% 長的樣子：

這是指數增長的相反， 「指數遞減曲線」。

那如果我們把「復原」這個條件加入S型邏輯增長的模擬中，會發生什麼事呢？

讓我們來試試看。

紅色曲線 是 現存 病例 ，
灰色曲線 是病例 總數 （現存＋治癒 ）， 開始只有0.001%的 ：

這 正是 那條有名曲線的由來！它不是鐘形曲線，它甚至不是一條「對數—常態分佈」曲線，它沒有名字，但你見過它無數遍，而且希望它扁下來。

這是 SIR 模型,⁵
(Susceptible （易感） Infectious （傳染） Recovered （復原） )
流行病學導論裡第二重要的概念：

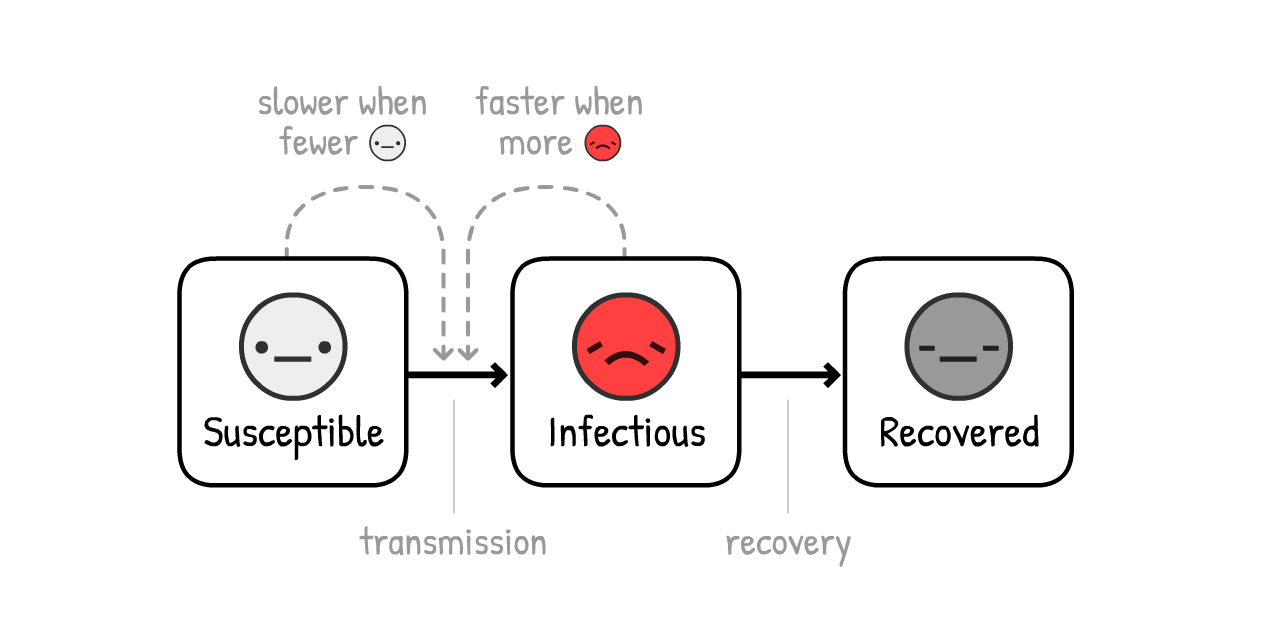
註：政策制定所需的模擬比這個 複雜得多 了！ 但SIR模型在大方向上仍是正確的，即使少了一些細節。

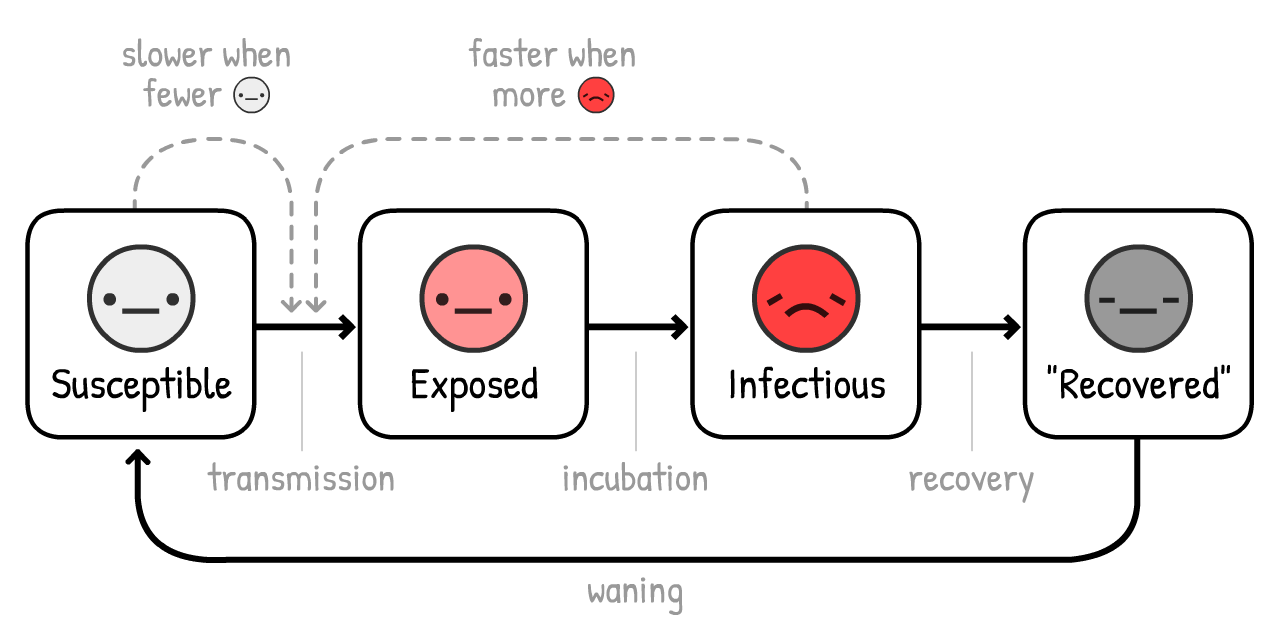
讓我們再加入一個小細節：在 變成 之前，他會先變成感染者 。

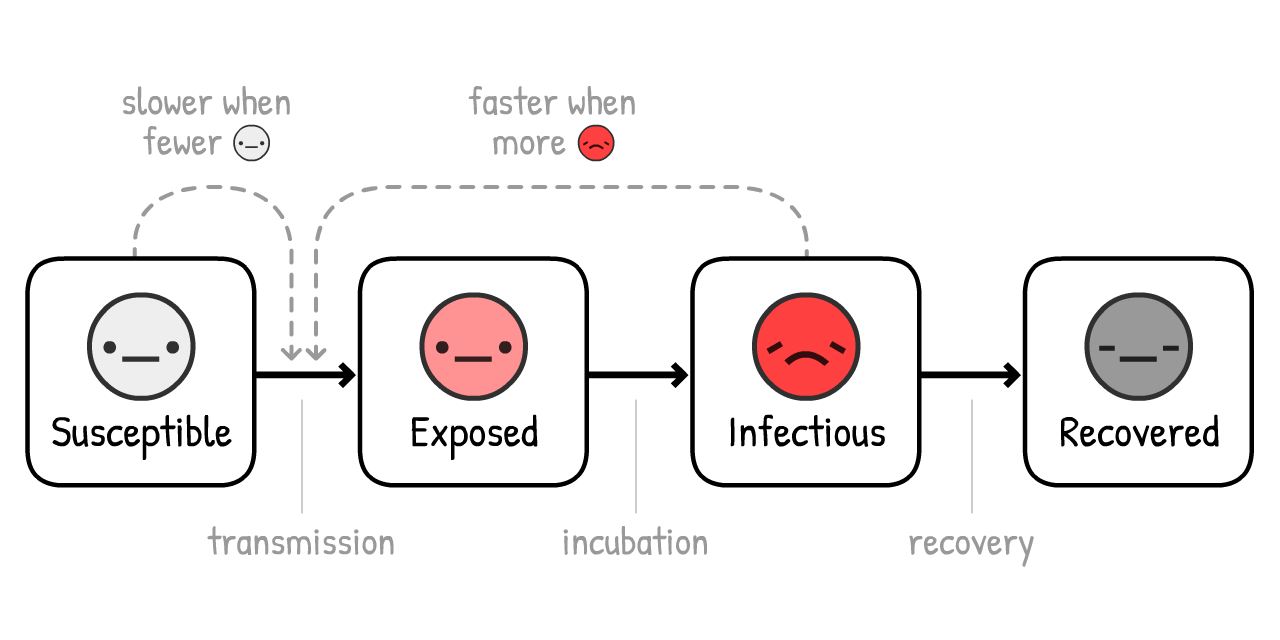
（這個變體叫做 SEIR 模型 ⁶，其中「E」代表「感染（Exposed）」。請注意這跟日常生活中「暴露於(Exposed)」（不管你有沒有得到病毒）的意思 並不一樣 。在這裡，「感染」的意思是你一定得到它了。科學用語很爛。）

根據估計，對於COVID-19來說，一個病人 處於被感染但仍未具傳染性的時間 平均 為3天，⁷加入這個參數對我們的模擬會產生什麼影響呢？

紅色 ＋粉紅色 曲線 是 現存 病例（傳染 ＋感染 ），
灰色曲線 是病例 總數 （現存＋康復 ）：

差別不大！ 處在潛伏期的長短會改變 與 的比例 和 現存病例 高峰出現的時間…，但高峰的 高度 和最後的感染總數不會變。

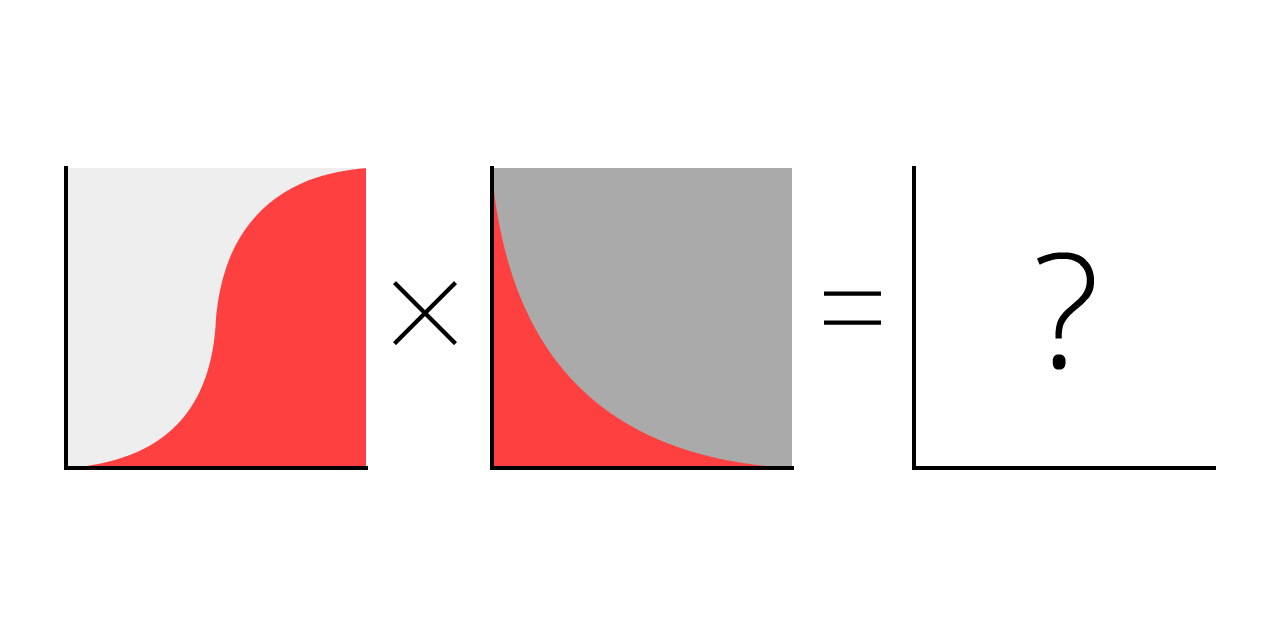
為什麼會這樣呢？這是因為流行病學101裡 最重要 的概念：

「再生數（Reproduction number）」的縮寫。這是一位在 康復前 （或死亡前）傳染的平均人數。

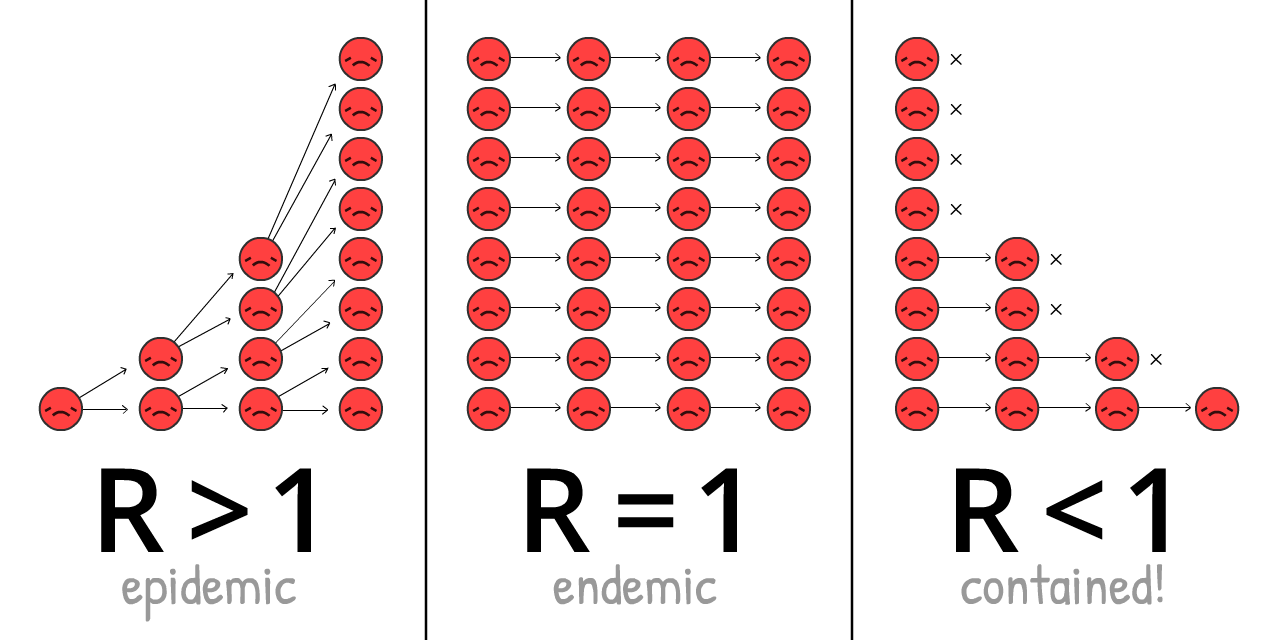
因著更多人免疫和人為干預， R 隨著疾病爆發的過程發生變化。

R₀ （唸作 R-nought）是R在疾病剛爆發時（未有免疫及干預）的值，R₀比較能反映病毒本身的感染力，但仍因地而異。舉例來說， R₀在人口稠密的都市比在人煙稀少的地方高。

（大部分的新聞文章（甚至某些研究論文！）混淆了R和R₀。再說一次，科學用語很爛。）

季節性流感的R₀值大約為1.28⁸，這意味著在 剛剛 流感爆發的時候，平均一位 傳染給1.28個人（如果你覺得這是小數很怪的話，記得「平均」一位母親有2.4個孩子，這不代表有半個孩子跑來跑去。）

2019-新型冠狀病毒的R₀估計為2.2⁹ ，雖然一份還未定稿的研究估計在武漢的R₀值為5.5（！）¹⁰。

在我們的模擬中（剛開始和平均來說）一位 十天裡，每四天會傳染給一個人。「四天」在「十天」裡經過2.5個週期，也就是說 （剛開始和平均來說） 傳染給2.5個人，所以R₀ = 2.5 （警告：¹¹）

玩玩看這個R₀計算機，看看R₀和康復時間和感染他人的時間的關係為何。

但記住， 越少， 越慢 成為 。 當下 的再生數R不只和 基本 再生數R₀有關，也和不再易感 的人數有關（例如經由康復和得到天然免疫力。）

當具有免疫力的人夠多的時候，R < 1，疫情被控制住了！這叫做 群體免疫（herd immunity） 。對流感的群體免疫是藉由 疫苗 獲得，藉由很多民眾被感染而取得「天然群體免疫」是很 糟糕 的想法（但可能不是你所想像的原因！我們會在之後解釋。）

讓我們再玩SEIR模型一遍，但這次顯示R₀、R隨時間的變化和群體免疫閥值：

註：病例總數並不會停在得到群體免疫的時間點，而是在這之後！而且群體免疫 正是在 現存病例的最高峰時產生的（這件事不隨參數改變，你自己試試看！）

這是因為當非大於群體免疫閥值的時候你會得到 R<1 ，而當 R<1 時候，新病例的增長速度減慢：也就是最高峰。

如果你只能從這份指南學到一件事的話，就是這件事 ——這是一個非常複雜的圖，所以請花時間好好吸收它：

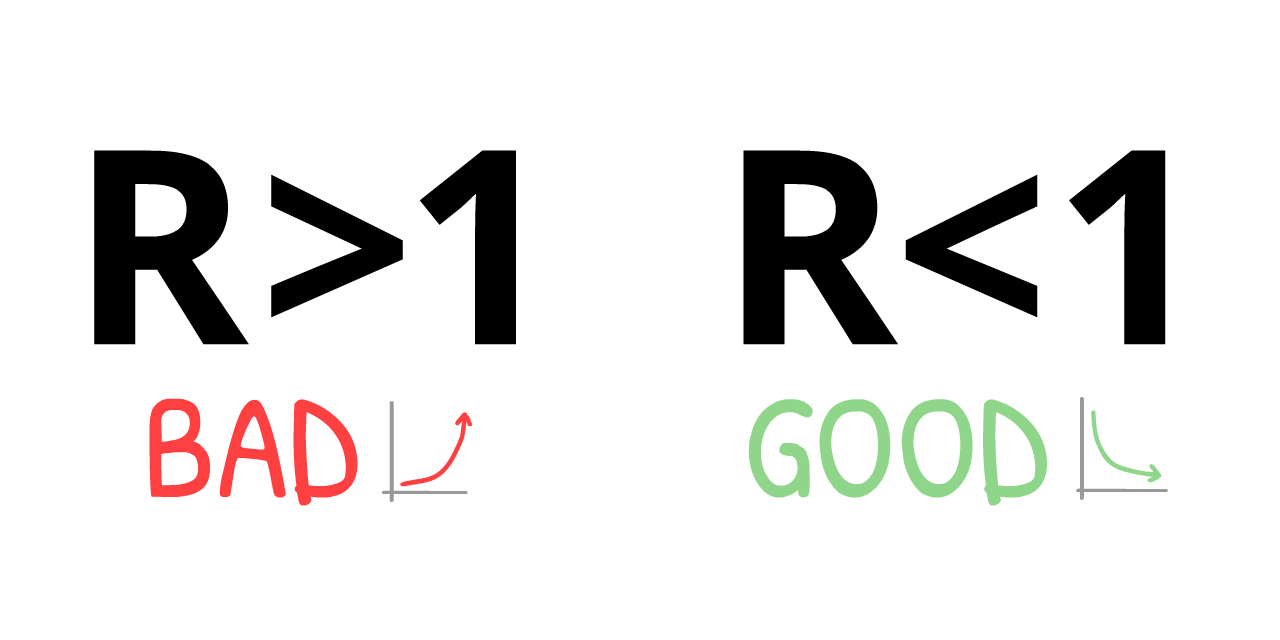
這代表：我們不需要找到所有或幾乎所有傳染途徑來阻止COVID-19！

這是個悖論，COVID-19的傳染性超級高，但我們「只需」降低60%的傳染就能遏止它。60%？！如果換算成學校成績的話，那代表D-的意思，但如果R₀=2.5的話，減少61%的傳染會讓我們得到R=0.975，也就是 R<1。病毒被遏制住了！（正確的公式：¹²）

（如果你覺得 R₀或模擬裡其它數字太低／太高的話，這很好，你在挑戰我們的假設！在這份指南的結尾我們提供一個「沙盒模式」，你可以在那裡試試 你自己 的數字然後看看會發生什麼。）

所有你聽過阻擋COVID-19的手段——洗手、社交／肢體距離、封鎖、自主隔離、接觸追蹤和隔離檢疫、戴口罩甚至「群體免疫」——它們都是為了同一件事：

讓 R < 1。

所以現在讓我們的「流行病飛行模擬器」來解答：如果在確保 心理健康 和 財政健全的情況下 讓 R < 1？

準備好緊急迫降⋯⋯

接下來的幾個月

⋯⋯事情可能會變更糟。接下來是我們避免的平行宇宙：

場景 0：什麼都不做

每20個感染新冠病毒的人有1個需要進到加護病房¹³。以美國為例的富裕國家，每3400個人會分到一張加護病房的病床¹⁴。因此美國能處理每3400人有20人得到新冠病毒的狀況——或0.6%的人口。

如果我們將負荷量提高到3倍以上來到2%，以下是我們 完全不做任何事 會發生的情況：

不好。

這是 3月16號倫敦帝國學院報告的結論：如果我們什麼都不做，加護病房會塞滿病人，而且80%的人口會被感染。 （記得：被感染總數會超越群體免疫）

即使只有0.5%的感染者死亡 ¹⁵ ——在沒有加護病房下很寬鬆的假設——在如美國一樣擁有3億人口的大國，3億中的80%中的0.5%仍代表一百二十萬人死亡⋯⋯ 如果我們什麼都不做的話。

（許多新聞或社群媒體報導「80%會被感染」卻不講 我們什麼都不做 。恐懼被轉化為點擊數而非理解。 唉 ）

場景 1: 拉平曲線／群體免疫

所有的公共衛生機構都在宣傳「拉平曲線」計畫，然而英國原本的「群體免疫」計畫卻受到滿堂倒彩。它們是 一樣的計畫。 只是英國政府的公關能力很糟。¹⁶

然而兩者皆具有致命的缺陷。

首先讓我們先來看一樣兩種主要「拉平曲線」的方法：洗手和肢體距離。

增加洗手率在高收入國家能減少約25%的流感與感冒¹⁷，而倫敦的全城封鎖減少了約70%的近距離接觸¹⁸。所以讓我們假設洗手能將R值降到 最多 25%，而社交距離能降低R值 最多 到70%

使用這台計算機來觀察非的百分比、洗手和距離政策如何降低R： （計算機是將它們之間的 相對 關係視覺化，這就是為什麼提高其中一個 看起來 降低了其它的效應¹⁹）

現在讓我們模擬以下對COVID-19疫情的影響：如果2020年3月增加洗手的比例，搭配些微的社交距離使得R雖然降低了，但仍高於1：

三點註記：

1. 這 降低 了病例總數！ 即使沒有達到 R < 1，降低R值仍舊能藉由降低群體免疫以上的病例數來拯救生命。 很多民眾覺得「拉平曲線」只是讓病例發生的時間散開了而沒有降低總數。這在 任何 流行病學101的模型裡都是不可能的。但因為新聞「80%+的人會被感染」報導得好像是不可避免的，民眾以為不管怎樣都沒辦法降低病例總數。 唉。

2. 由於採取了額外的干預措施，目前的病例在「群體免疫」之前達到「高峰」。實際上，在此模擬中，總病例僅比群體面議高一點點-這就是英國的計劃！此時 R < 1，不需要其它的干預措施，而且COVID-19的疫情保持控制！ 好吧，除了一個問題...

3. 加護病房還是會在幾個月後被用光（而且記得，我們 已經 在這些模擬裡把加護病房數增加3倍。）

這是帝國學院3月16日報告的另一個發現，說服英國放棄原本的計畫。任何嘗試 緩和 （降低R但R > 1）疫情的嘗試都將失敗，唯一的解決辦法是 抑制 疫情（將R值降到<1）。

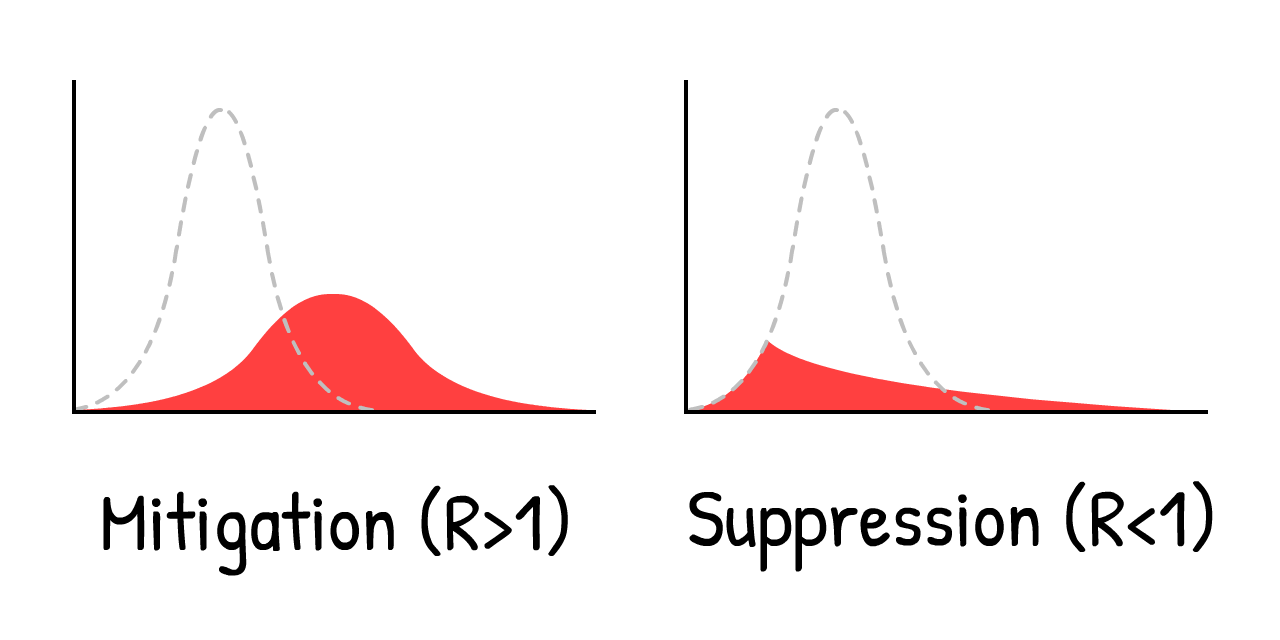
也就是說不要緊緊「拉平」曲線。「壓扁」它。舉個例子，用⋯⋯

場景2：幾個月的封鎖

讓我們看看如果我們用5個月長的封鎖將曲線 壓扁 ，將降到幾乎為0，然後最後—— 終於 ——回到正常生活：

喔。

這就是大家說的「第二波疫情」：一旦解除封鎖，我們將再次得到R > 1。所以任何一條漏網之魚 （或移入的）都會造成病例突然增加，這幾乎和場景0——什麼都不做——一樣糟。

封鎖不是解藥，它只是開始。

那又怎樣，不然我們一直重複封鎖怎樣？

場景3：間歇性封鎖

這個解決辦法在帝國學院3月16號的報告第一次被建議，然後再次在哈佛的論文裡被提出來。²⁰

模擬在這： （當你嘗試完「預設情況」後，你可以在模擬運行時移動滑桿來試試自己的封鎖時程！記得你可以暫停和繼續模擬，也可以改變模擬的速率。）

這 會讓 病例數低於加護病房容量！而且這比持續至疫苗上市的18個月封鎖要 好多了 。我們只需要⋯⋯封鎖幾個月，解除封鎖幾個月，持續至疫苗問世（而如果一直沒有疫苗，持續至⋯⋯2020年達到群體免疫）。

注意，畫一條代表「加護病房容量」的線很好，但在這裡我們有很多重要的事情 沒辦法 模擬，例如：

心理健康： 孤獨是造成憂鬱、焦慮和自殺的重要因子，而且它造成早死的效應等同每天抽15根菸。 ²¹

財政健全： 「那經濟怎麼辦」聽起來像是你在乎鈔票多餘人命，但是「經濟」不僅限於股票：它還包含了人們提供食物和居所給他們所愛的人的能力、投資孩子的未來、和享受藝術、美食、電玩——那些使人值得活著的事物。除此之外，貧窮 本身 會帶來對身心健康的可怕影響。

我們並不是在說我們 不該 再次封鎖！我們將會在之後討論「斷路器式」封鎖，但這仍不是理想的辦法

但等一下⋯⋯台灣和韓國不是 已經 在沒有長期封鎖的情況下遏制COVID-19了嗎？

它們怎麼做到的？

場景4：檢驗、追蹤、隔離

當然我們 應該 在開始的時候跟台灣和韓國做一樣的事情，但現在已經太晚了，我們已經錯過開始的時間。

但這就是重點！「封鎖不是解方，它只是重新開始⋯⋯」 而一個全新的開始正是我們需要的。

要了解台灣和南韓遏制疫情的方法，我們需要瞭解一般COVID-19的感染病程²²:

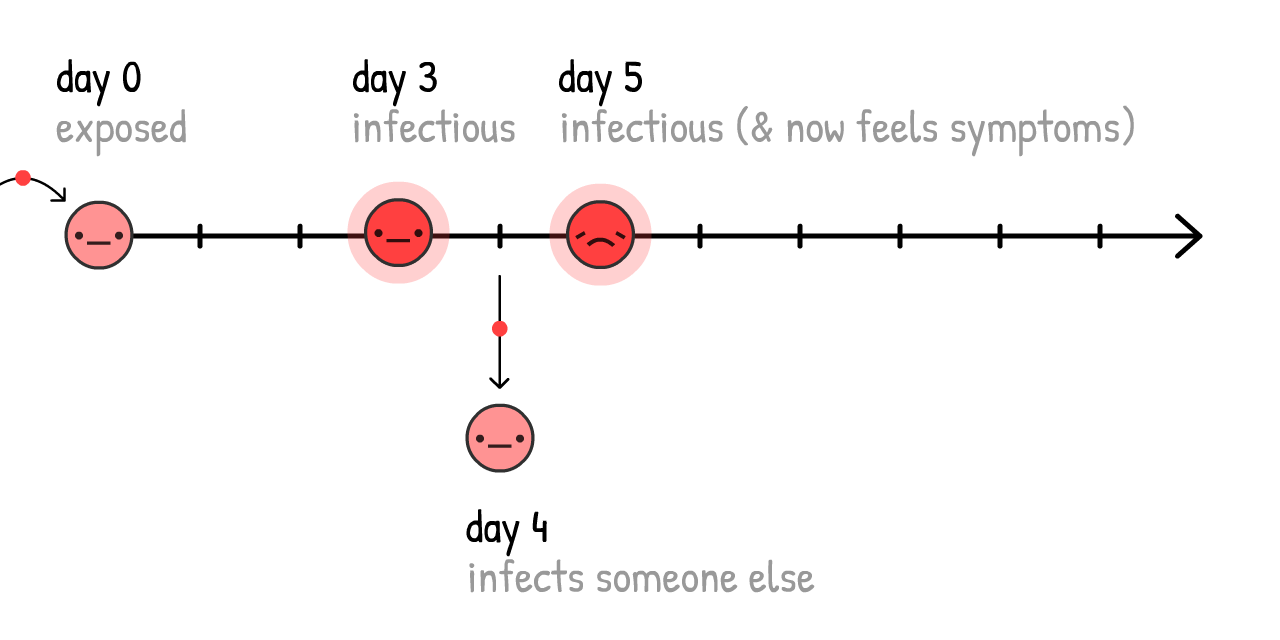
如果人們在知道他們自己生病了才自主隔離（也就是說他們發覺症狀），那病毒還是能夠散播：

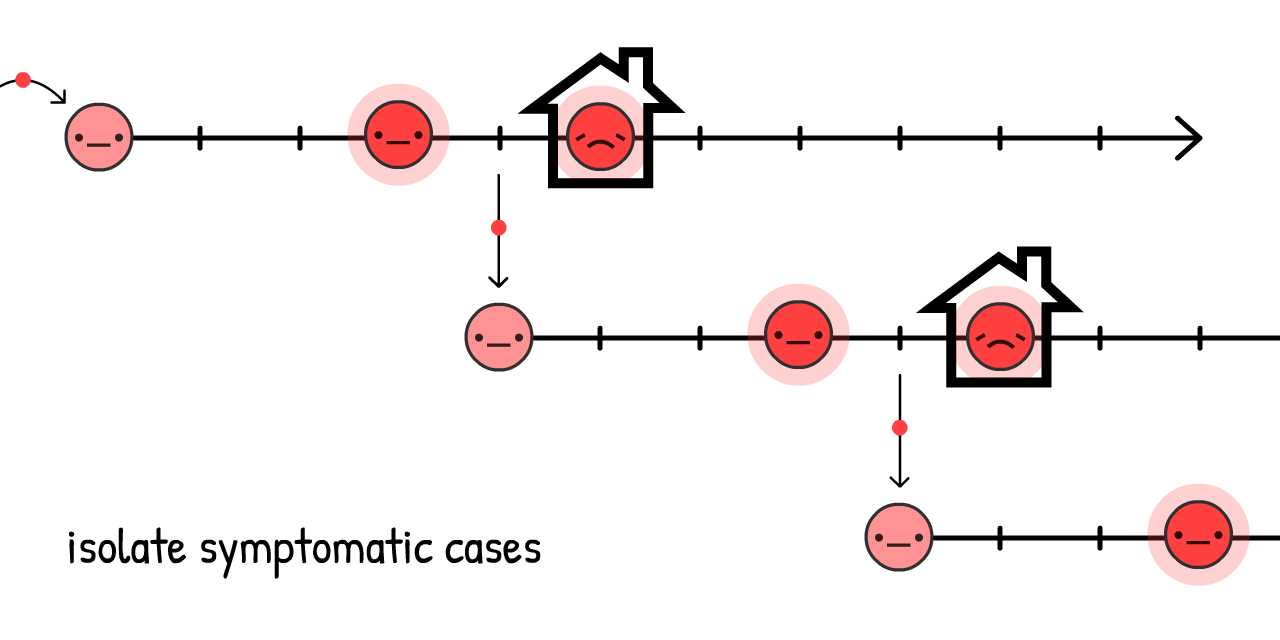
而且事實上44%的傳播就是這樣來的：在症狀發生之前！ ²³

但如果我們找到 並隔離 出現症狀的病患最近所接觸的人⋯⋯我們就能藉由超前部署來阻止疾病傳播開來！

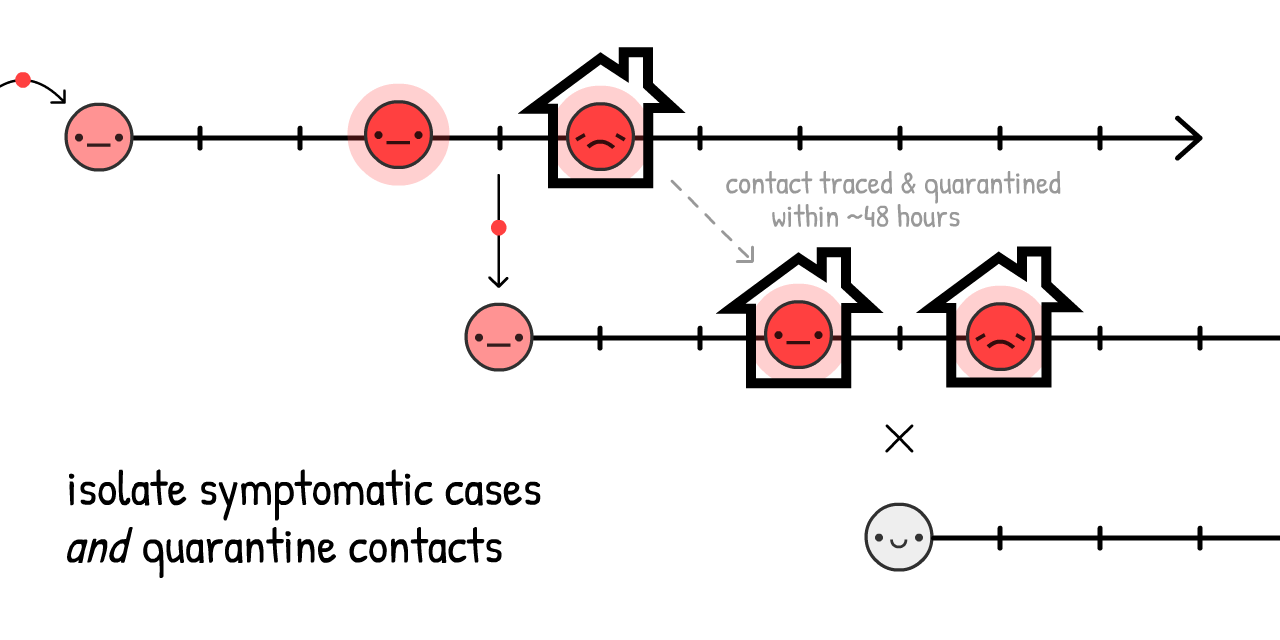
這叫做 接觸者追蹤 。它是一個老想法，曾以史無前例的規模被用來遏制伊波拉 ²⁴ ，如今成為台灣和南韓遏制COVID-19的核心部分。

（這也讓我們更有效率地實施我們有限的測試，在不需檢驗幾乎所有人的情況下找到處於傳染期的患者。）

傳統上接觸者是在訪問病患的過程中被找到的，但只利用這些對COVID-19約48小時窗口來說太慢了。這是為什麼接觸追蹤者需要幫忙，並需要接觸追蹤app的幫助——不是被取代。

(這個想法並不是來自「科技宅」：最早是一個牛津流行病學家的團隊提出使用app來對抗COVID0-19的方案。)

等等，追蹤你曾接觸過的人的app⋯⋯？這是不是代表放棄隱私權然後交給老大哥？

當然不是！ DP-3T ，一組流行病學家與密碼學家的團隊（包含我們的其中一員Marcel Salathé） 已經 在開發一款接觸追蹤app——原始碼公開——，它 不會揭露你的身份、位置、和你接觸的人甚至你 曾接觸的人數 。

以下是它的原理：

(這裡可見完整的漫畫。關於「惡搞」／偽陽性／等等請見註腳： ²⁵ )

與其他相似的團隊如TCN協議²⁶與MIT的PACT²⁷，他們啟發了蘋果和Google直接將隱私權優先的接觸追蹤植入Android/iOS²⁸ （不相信Google/蘋果？很好！這個系統美妙的地方是它 不需要 信任！）不久之後，你的地方衛生機構可能會要求你下載一款app，如果它是隱私優先且原始碼公開的軟體，請這麼做！

但那些沒有智慧型手機的民眾怎麼辦？或者感染源是門把怎麼辦？或「真正」無症狀的病例？接觸追蹤app沒辦法抓到所有的傳染源⋯⋯ 沒有關係！ 我們不需要抓到 所有的 感染源，只需要60%+即能達到 R < 1。

（註腳是關於混淆未產生症狀與「真正」無症狀感染的抱怨——真正的無症狀感染很罕見：²⁹）

隔離 出現症狀 的病例能將R降低最多40%，而隔離他們處於潛伏期／沒有症狀的接觸者能將R降低最多50%³⁰:

因此，即使沒有將100%的接觸者隔離起來，我們還是能在 沒有封鎖 的情況下得到 R < 1！對心理健康和經濟要好多了。（對那些需要自主隔離／隔離檢疫的民眾， 政府應該要補助他們的花費 ——包含檢測費用、工作保障、提供有薪假等等。仍然比間歇性封鎖要好多了。）

然後我們維持R < 1直到疫苗問世，將可感染的變成免疫的。用 正確的 方法達到群體免疫：

（註：這個計算機假設疫苗百分之百有效。只要記得在現實中，我們需要施打 大於 「群體免疫」數量的疫苗來 真正 的群體免疫。）

好了，廢話夠了。以下是這些情況的模擬：

1. 數個月的封鎖，直到我們可以⋯⋯
2. 轉變成「檢測、追蹤、隔離」直到我們可以⋯⋯
3. 給夠多人施打疫苗，這意味著⋯⋯
4. 我們贏了。

就是這樣！這就是我們如何將飛機緊急迫降。

這就是我們如何打敗COVID-19。

...

但如果事情 仍然 往不好的方向發展呢？事情已經很糟了。這是恐懼，這很好！恐懼給我們力量制定 備案 。

悲觀者發明降落傘。

場景4+：全民戴口罩、夏天、斷路器

如果R₀比我們想的要高得多，而且以上所有的手段，甚至是輕微的距離規範，仍沒有辦法讓 R < 1呢？

記住，即使我們沒辦法讓 R < 1，降低R值仍然能夠減少病例總數，因此挽救生命。即使是這樣，R < 1仍然是理想的情況，所以這裡提供其他降低R的方法。

全民戴口罩：

等等 你可能想： 「我以為口罩沒辦法避免人生病？」

你是對的。口罩沒辦法避免你生病³¹⋯⋯他們避免你將病傳染給 別人 。

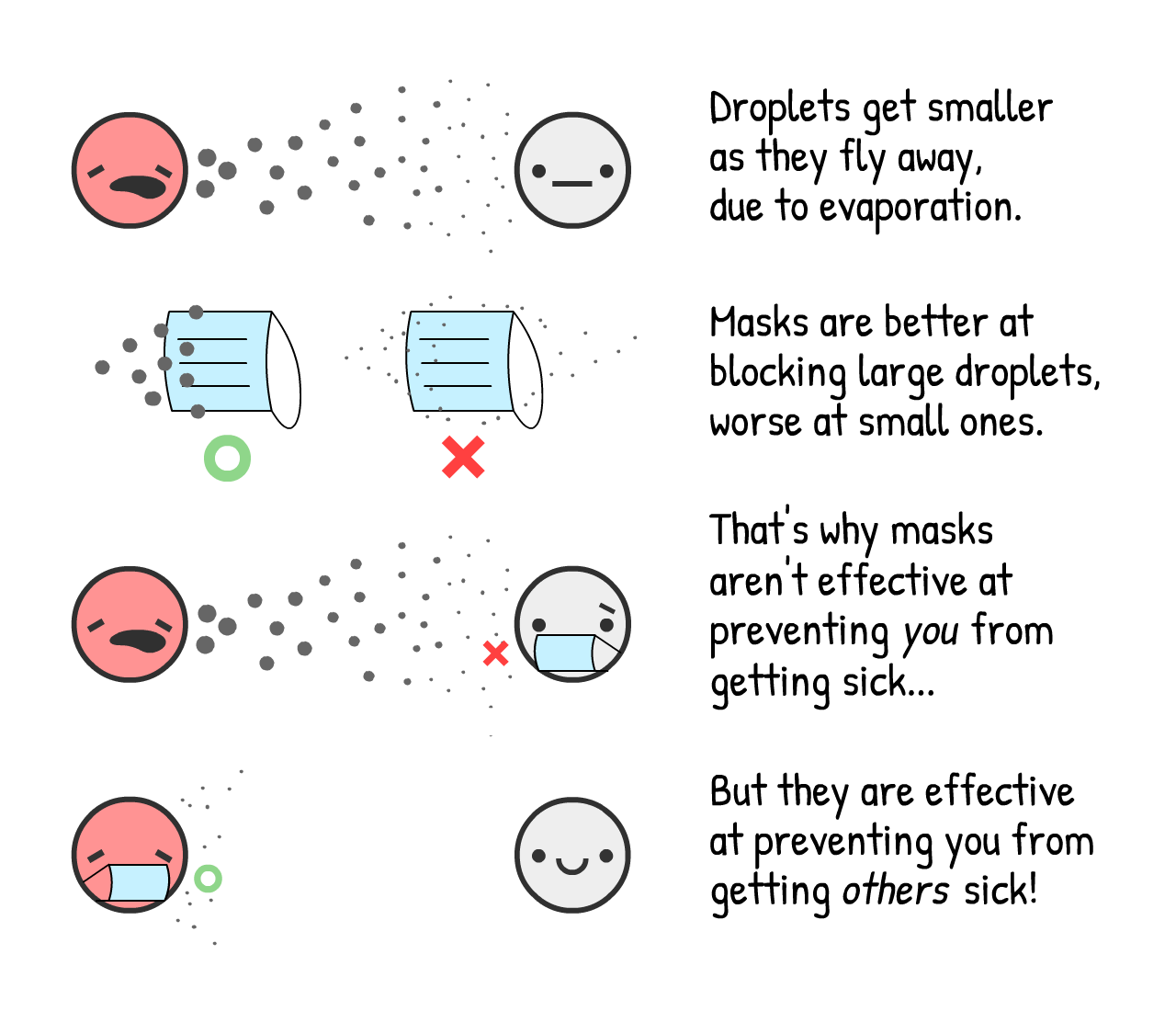
我們把這些效應量化： 患者戴口罩 減低感冒和流感病毒氣膠的70%。³²傳染率減低70%代表和封城的效應一樣大！

然而我們並不知道口罩 針對 COVID-19的效應有多大，科學上我們只應該發表有95%信心的發現。（⋯⋯應該。³³）在2020年5月1日我們對於口罩的效應只有「低於95%的信心」。

但對付疫情就像牌局， 如果要等到有百分之九十五的把握才要下注，那在賭局中你將輸得很慘 正如一篇近期在英國醫學期刊(BMJ)關於口罩的論文提到的³⁴，我們 必須 在不確定中做利弊分析。像這樣：

成本：如果自製衣物口罩（效用大約是醫用口罩的2/3³⁵），超級便宜。醫用口罩比較貴但還是很便宜。

好處：即使假設只有5成的機會醫用口罩能降低70%的傳播，5成的機會它們完全沒用， 期望值 仍舊是35%，這跟半封城的效果一樣！因為不確定性，我們猜測醫用口罩能降低R值最多至35%（再一次說你可以藉由改變參數來挑戰我們的假設）。

（其它支持／反對口罩的論點：³⁶）

「口罩很難戴得正確。」 照世衛指南洗手也很困難——認真的，「第三步：右手掌在左手背上」？！——但我們仍然建議洗手，因為不完美仍比什麼都不做好。

「這會讓人們更輕忽洗手和社交距離。」 的確，安全帶讓人們忽略交通號誌，牙線讓人們亂吃。但認真說，我們會往相反的方向論證：口罩是一個實體化的提醒——而且在東亞，口罩是團結的象徵！

單單使用 口罩沒辦法達到 R < 1。但如果洗手加「檢驗、追蹤、隔離」將R降低至1.10，只需1/3的人戴口罩就能將R降到1以下，成功遏制病毒！

夏天：

Okay，這不是我們能掌握的「手段」，但這會有幫助！一些新聞報導指出夏天不會對疫情造成任何影響，他們只對一半：夏天不會讓 R < 1，但 會 降低R。

對COVID-19來說，每增加攝氏1度（華氏1.8度）會讓R值降低1.2%。³⁷紐約市夏冬溫差是攝氏26度（華氏47度）³⁸，所以夏天會讓R降低約31%。

夏天本身不會讓 R < 1，但如果我們只有有限的資源，我們可以在夏天花少一點——這樣我們為冬天做預備。

「斷路器式」封鎖：

如果這一切都沒辦法讓 R < 1⋯⋯我們還是能再封鎖一次。

但我們不需要在持續兩個月封鎖／一個月解封的循環！因為R已經被降低了，我們只需要在疫苗問世前實施一兩次「斷路器式」的封鎖即可（最近新加坡就不得不這麼做，「雖然」他們已經控制疫情四個月了。這不代表失敗：這是成功的 代價 。）

以下是一個「懶惰例子」的模擬：

1. 封鎖，然後
2. 適度的衛生＋「檢測、追蹤、隔離」＋適度的全民口罩政策，然後
3. 在疫苗問世前再一次「斷路器式」的封鎖。

不要說我們還有 一堆 手段可以再進一步壓制R：

• 旅遊限制／隔離檢疫
• 在商場和學校量測體溫
• 公共場所全面消毒
• 將握手改為碰腳
• 和其它一切人類的創造力將帶來⋯⋯

我們希望這些計畫能帶給你希望。

即使在悲觀的情況，在保全心理健康和經濟的前提下打敗COVID-19仍是可能的。 將封鎖視為「重啟鍵」，用隔離病患來保持R值小於1＋保護隱私的接觸追蹤＋口罩（至少自製口罩）⋯⋯生活可以幾乎回歸正常！

當然，你可能會有雙乾裂的手，但你可以到漫畫店約會！你可以和朋友出門去看最新的好萊塢大戲。你可以去圖書館觀察人群，享受人們 活著 從事日常事務的喜悅。

即使在最壞的情況下⋯⋯生命仍能堅持下去。

所以讓我們為 最壞 的幾個情況做計畫。我們會在水面降落，準備好你的救生衣，跟隨指示燈到緊急逃生口：

接下來的幾年

你得到COVID-19並且復原了，或者你接種了疫苗。不管哪種情況，你現在都有免疫力⋯⋯

⋯⋯ 能持續多久？

• COVID-19最親近的近親為SARS，SARS的倖存者有2年的免疫力。 ³⁹
• 造成普通感冒的冠狀病毒會給你8個月的免疫力。 ⁴⁰
• 有些患者從COVID-19康復然後再被檢測出陽性，但目前我們仍不清楚這是不是偽陽性。⁴¹
• 一篇還未經同行審查關於猴子的研究顯示對新冠病毒的免疫力至少能持續28天。⁴²

但人體對COVID-19的免疫力 有多長 ，在2020年5月1日的現在仍舊是大哉問。

讓我們假設在接下來的模擬時間為1年 這個模擬從100% 開始，在 平均 一年後指數遞減為易感或沒有免疫力（可能有些變異數）：

指數遞減回歸！

這叫 SEIRS模型 。最後的S還是代表易感(susceptible)病患。

接下來讓我們模擬在 免疫力只持續1年的假設下 ，接下來的十年爆發COVID-19疫情並且沒有干預手段的情況：

在之前的模擬，我們只會得到 1個 加護病房過滿的尖峰，現在我們得到數個 而且 將 一直 佔住加護病房（記得我們已經將加護病房容量增加3倍了）。

R = 1， 這是 流行(endemic)。

幸好，因為夏天會降低R值，這會讓模擬好一些：

喔。

違反直覺地，夏天讓這些尖峰變得更糟而且頻繁發生！這是因為夏天將降低，但同時也減低了新增免疫的人數。這意味著免疫人數在夏天驟減，在冬天 製造 新的尖峰。

幸好解決方案相當直接——只要在秋冬讓民眾接種疫苗，如同我們對付流感所用的流感疫苗：

（在試完預設參數後，試試看你自己的疫苗計畫！記得你可以隨時暫停或繼續模擬）

但接下來有個更嚇人的問題：

如果接下來的 數年 或 永遠 都沒有疫苗？

我們要澄清：這個機會不大。 多數流行病學家認為疫苗將在1到2年出現。的確從來沒有對付冠狀病毒的疫苗，但這是因為SARS很快就被撲滅了，而造成普通感冒的冠狀病毒不值得疫苗投資。

但流行病學家仍然提出擔憂：如果我們沒辦法製造夠多疫苗呢？⁴³ 如果我們趕製出來而它並不安全呢？⁴⁴

即使在「沒有疫苗」的惡夢場景下，我們仍有3個解套辦法：從最嚇人到比較沒那麼可怕的：

1) 採取間歇性封鎖或寬鬆的R < 1干預手段來達到「自然群體免疫」（警告：這會造成很多死亡及肺損傷案例）。 而且 如果免疫沒辦法持續這個方案不會有效。

2) 永遠採取R < 1干預手段。接觸追蹤和戴口罩成為後COVID-19世界的新日常，如果性病檢查和戴保險套成為後愛滋世界的新日常。

3) 採取R < 1干預手段直到我們開發出讓COVID-19重症出現的機率遠遠降低（這是我們無論如何都應該做的！）。將重症率降低10倍相當於增加10倍的加護病房數：

接下來的模擬假設 沒有 永久免疫、 沒有 疫苗甚至沒有任何干預手段，只有增加度過長期尖峰所需的容量：

即使在最糟的幾個情況中最壞的那個⋯⋯生命仍能堅持下去。

...

也許你想嘗試使用不同的R₀或數字，或嘗試模擬你自己的干預計劃組合來挑戰我們的假設！

接下來模擬是沙盒模式， 所有的 參數都列出來了（下滑來看到所有參數），模擬和嘗試你心中的想法：

這個基本的「流行病飛行模擬器」已經教會我們很多事情，它讓我們能回答過去幾個月、接下來幾個月和接下來幾年會遇到的問題。

最後，讓我們回到⋯⋯

現在

墜機了，我們爬上了救生筏，現在是找到陸地的時候了。⁴⁵

許多流行學家和政策制定者的團隊（左派、右派和跨黨派）已經達成在保全我們的生活 及 自由的前提下，如何打敗COVID-19的共識。

以下是基本的想法，以及一些（比較沒有共識）的備案：

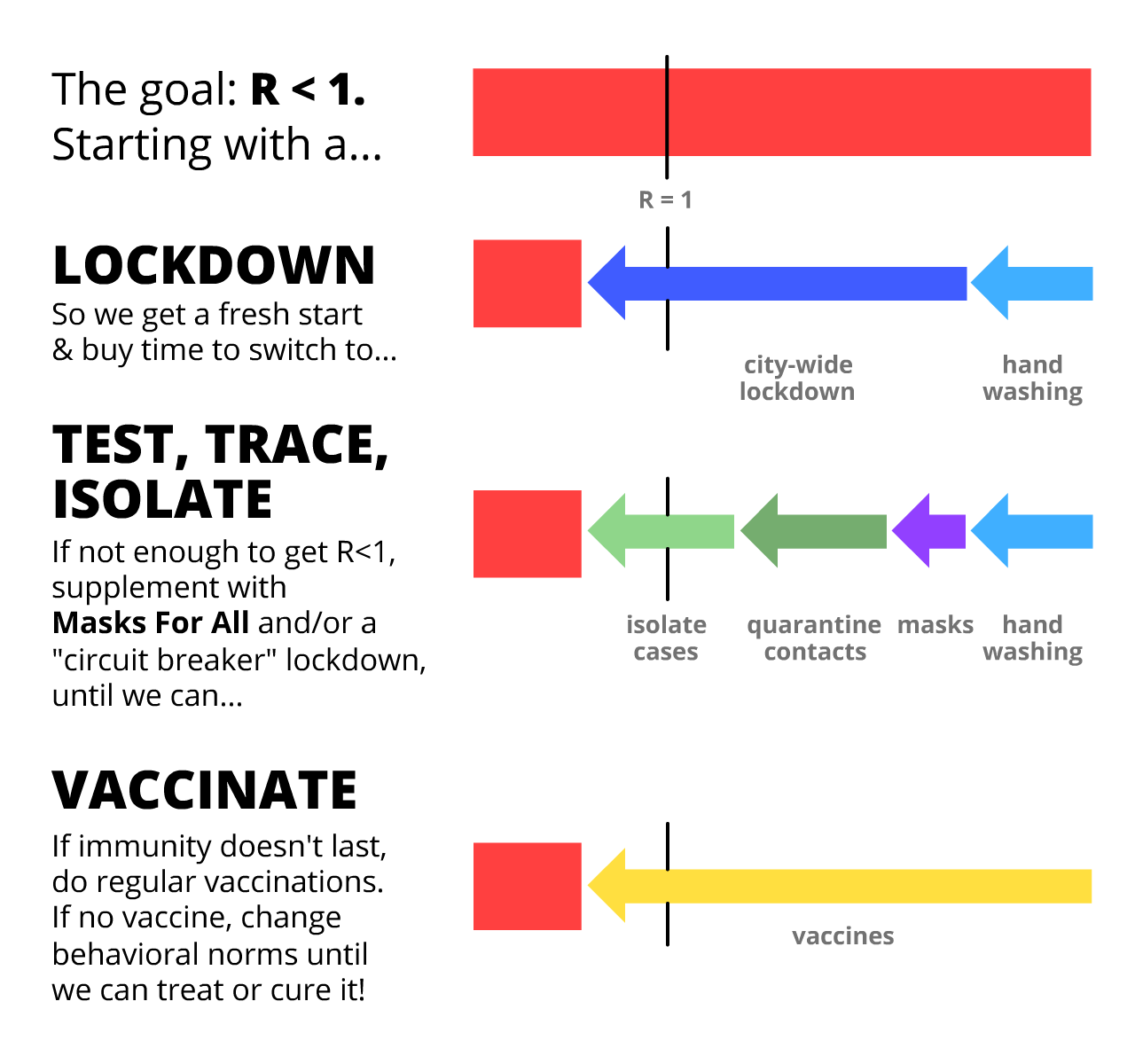
所以這對你在這個當下的意義是什麼？

給所有人： 遵守封城規定讓我們能越快脫離第一階段越好、持續洗手、製作你自己的口罩。在下個月保護隱私的接觸追蹤app問世時下載他們。保持身心健康！寫信給你的地方決策者，叫他們開始行動⋯⋯

給決策者： 制訂支援需要自主隔離／隔離檢疫的民眾。雇用更多接觸追蹤員，並讓接觸追蹤app協助他們。提供更多資金讓我們可以製作⋯⋯

給建造者： 製作測試，製造呼吸器，製造給醫院的個人保護用具，製作測試，製造口罩，開發app，製作抗病毒藥物、預防藥物和其它非疫苗的治療，製作疫苗，製作測試，製作測試，製作測試，建立希望。

不要用壓制恐懼來建立希望。我們的恐懼應該和希望用在一起，如同飛機和降落傘的發明人。為恐怖的未來做準備是我們如何 產生 有希望的未來。

唯一需要恐懼的是恐懼的想法。